All the threads dealing with the physics so far used arrows as an example, for a very simple reason: the arrow can very easily, and without neglecting any mayor details, be viewed in a vacuum, which just doesn't work as well for melee weapons.
Melee weapons give us two problems to solve before we can estimate their kinetic energy or their momentum:
With how much mass are we effectively striking/cutting/thrusting.
For striking and cutting this is problematic, because we are obviously not using the full weight of the whole thing. Think of a sword ... the mass of the hilt will not help you with your cut as much, as if we had that mass somewhere closer to the point of impact.
How fast does this effective mass move.
For an arrow it is pretty easy to determine how fast it is going to move, once we know how much energy the bow will exert on it, and how heavy it is. For melee weapons this is a bit more tricky ... the point of impact is not moving at the same speed as our arms, besides, how fast do our arms even move?
How much mass does your body add to the effective mass
This last point is also the most difficult to solve. (It's pretty simple for thrusts though.) Using a melee weapon involves your whole body, it's not just your arms, so if nothing else, we add some momentum and maybe a tiny bit of mass to the whole ordeal.

(not to scale)
Here you can see a solution for our first problem ... atleast for this specific sword. Luckily it is a bit easier to get a good estimate for axes, maces and all sorts of other top heavy weapons ... you just take the weight of the head, and add between 0.1-0.25 kg, depending on how long and heavy the shaft is. As you can see we already have to start estimating stuff, so keep in mind we will only get a rough approximation in the end.

Next up we will take this guard position (I think it's a side guard, but he is holding the sword pretty far over his shoulder) as the example on how to estimate the speed of the point of impact.
We want our point of impact to be 1 m up from the hilt in this scenario (0.8 m from the center of mass), so whatever movement the swordsman makes the point of impact is on a lever of 1 m length.
We could try to estimate how fast the swordsman can move, based on how fast the muscles used for a normal strike with a two-handed weapon can contract, but I guess that is something we can do another time, in threads dealing with specific weapons. For now lets just compare his motion to something where we know the speed of the movement ... the example I'd choose is a baseball bat.
While I as a European am not overly familiar with baseball, I could find a nice chart showing (average) swing speed in relation to bat weight.
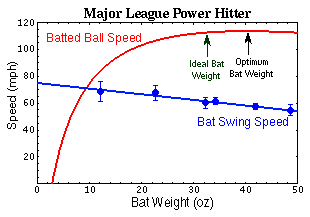
Mimicing the motion of a cut (Edit.) my hands moved 1 m, on a circle with .65 m radius (that's the length of my arm).
The bat strikes about .7m from the hands. So in the time my hands moved 1 m, the point of impact, moves ~2.08 m. Since we know how fast a baseball bat of 50 oz. Weight moves, and we know the distance it would move, we can calculate the time it takes to swing it: 0.0788 seconds.

So, now to convert all this to our example. The sword in our first graphic weighs about 50 oz., so the velocity for the baseball bat should be the same for our sword - atleast 0.7 m from my hands. We want to strike with a point 1 m from the hilt though. Thus the distance the point of impact covers in .079 seconds is close to 2.55 m. From this we can calculate the velocity of the point of impact, and combined with the apparent mass from our first chart we can calculate the kinetic energy:
0.5 x 0.6 x (32.28)² = 312.6 Joule
This might seem like a lot after seeing how much energy a bow generates, but keep in mind, a sword usually has a much larger area of impact than an arrow, so even with this much energy we won't achieve the same degree of armor penetration.
We also have to keep in mind the third point mentioned above. We merely calculated what amount of kinetic energy a sword moving that way would have at a given point of impact. What we didn't include was how much our own mass helps cutting. So the actual force generated will usually be higher.
For thrusts the whole thing is a bit easier ... we don't have a lever, our bodies involvement is clear, we can easily determine the velocity, and the area of impact is a whole lot smaller, and thus more similar to an arrow.
I hope this thread helped clear some stuff up, even though it seemed a bit convoluted, even to me while writing it, which is mostly because melee combat sadly doesn't have as many ressources to draw from as archery has, which made a lot of educated guesses a necessity.
If any of my assumptions are completely wrong, I apologize, and would ofcourse like to be shown how it is supposed to work.
Edit: we can also add a step to the whole thing. This would add another ~4 m/s to the velocity of the sword, increasing the KE to 394.9 Joule, aswell as providing more momentum.
Back to the collection thread




















